In a Problem Statement, You Can Limit Complexity by Making ____________.ã¢â‚¬â€¹

two.7: The Precise Definition of a Limit

1. Last updated

2. Save as PDF

Page ID

10233

By now you have progressed from the very informal definition of a limit in the introduction of this chapter to the intuitive understanding of a limit. At this signal, you should accept a very strong intuitive sense of what the limit of a function ways and how you can find information technology. In this department, we catechumen this intuitive idea of a limit into a formal definition using precise mathematical language. The formal definition of a limit is quite possibly one of the most challenging definitions you will encounter early in your study of calculus; still, information technology is well worth any effort you make to reconcile it with your intuitive notion of a limit. Understanding this definition is the key that opens the door to a ameliorate understanding of calculus.

Quantifying Closeness

Before stating the formal definition of a limit, we must introduce a few preliminary ideas. Recall that the distance between two points a and b on a number line is given past |\(a−b\)|.

• The statement \(|f(x)−L|<ε\) may exist interpreted every bit: The altitude between \(f(x)\) and L is less than \(ε\).
• The argument \(0<|x−a|<δ\) may be interpreted every bit: \(x≠a\) and the distance between \(x\) and \(a\) is less than \(δ\).

It is also important to look at the following equivalences for absolute value:

• The argument \(|f(ten)−L|<ε\) is equivalent to the argument \(L−ε<f(10)<50+ε\).
• The statement \(0<|x−a|<δ\) is equivalent to the statement \(a−δ<x<a+δ\) and \(x≠a\).

With these clarifications, we tin can state the formal epsilon-delta definition of the limit.

Definition: The Due eastpsilon-Delta Definition of the Limit

Let \(f(x)\) exist defined for all \(x≠a\) over an open up interval containing a. Let L be a real number. Then

\[\displaystyle \lim_{x→a}f(x)=L\]

if, for every \(ε>0\), in that location exists a \(δ>0\), such that if \(0<|x−a|<δ\), so \(|f(10)−50|<ε\).

This definition may seem rather complex from a mathematical point of view, simply it becomes easier to understand if we break it down phrase past phrase. The statement itself involves something called a universal quantifier (for every \(ε>0\)), an existential quantifier (at that place exists a \(δ>0\)), and, last, a provisional statement (if \(0<|ten−a|<δ\), then \(|f(x)−L|<ε)\). Let's take a await at Table, which breaks downward the definition and translates each office.

Definition	Translation
i. For every \(ε>0\),	1. For every positive distance \(ε\) from \(Fifty\) ,
2. there exists a \(δ>0\),	two. In that location is a positive distance \(δ\) from \(a\) ,
three. such that	3. such that
four. if \(0<|ten−a|<δ\), then \(|f(10)−L|<ε\).	4. if 10 is closer than \(δ\) to \(a\) and \(10≠a\), and then \(f(x)\) is closer than \(ε\) to \(50\) .

Nosotros can go a ameliorate handle on this definition by looking at the definition geometrically. Effigy shows possible values of \(δ\) for diverse choices of \(ε>0\) for a given function \(f(x)\), a number a, and a limit 50 at a. Notice that as we choose smaller values of ε (the distance between the office and the limit), we can always find a \(δ\) small enough so that if nosotros accept chosen an x value within \(δ\) of a, and then the value of \(f(ten)\) is within \(ε\) of the limit L.

Effigy \(\PageIndex{ane}\): These graphs show possible values of \(δ\), given successively smaller choices of ε.

Algebra Notes

An important algebra fact for absolute values yous will demand for proofs with the epsilon-delta definition of limit is:

\(|p|<k\) is equivalent to \(-g < p < one thousand\)

An algebra fact for inequalities is:

If \(a>0\) and \(b>0\) and so \(a<b\) is equivalent to \(\frac{1}{a} >\frac{1}{b}\)

Example \(\PageIndex{1}\) shows how y'all can utilize this definition to show a argument almost the limit of a specific function at a specified value.

Example \(\PageIndex{one}\): Proving a Statement virtually the Limit of a Specific Office

Prove that \(\displaystyle \lim_{ten→i}(2x+i)=iii\).

Solution

Allow \(ε>0\).

The beginning role of the definition begins "For every \(ε>0\)." This means nosotros must bear witness that any follows is truthful no matter what positive value of ε is chosen. By stating "Allow \(ε>0\)," we signal our intent to practise so.

Choose \(δ=\frac{ε}{2}\). Why are we choosing this? The explanation follows.

The definition continues with "there exists a \(δ>0\). " The phrase "there exists" in a mathematical statement is always a signal for a scavenger hunt. In other words, we must go and find \(δ\). So, where exactly did \(δ=\frac{ε}{ii}\) come from?

We tackle the problem from an algebraic bespeak of view. This is our "Analysis Putter" to observe what value to use for \(δ\).

Analysis

Since ultimately we want |(\(2x+ane)−3|<ε\), we begin by manipulating this expression: |(\(2x+1)−iii\)|<ε is equivalent to |\(2x−2|<ε\), which in turn is equivalent to \(-ε<2x−two<ε\) (run across Algebra Note above) which is equivalent to \(-\frac{ε}{2}<x−one<\frac{ε}{two}\). Last, this is equivalent to \(|10−1|<\frac{ε}{2}\). We desire \(|x−1|\) considering we accept x→i in this limit; \(δ\) is specifying how close \(x\) must be to \(1\). Thus, it would seem that \(δ=\frac{ε}{2}\) is appropriate. (end of Analysis Putter)

Effigy \(\PageIndex{2}\) demonstrates our epsilon-delta setup:

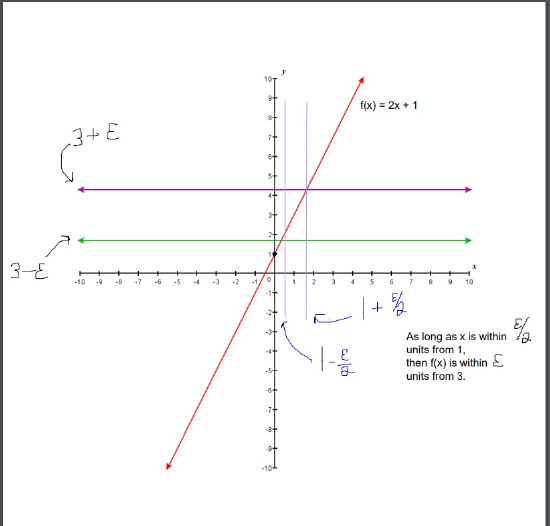
Figure \(\PageIndex{ii}\): demonstrates our epsilon-delta setup for \(\displaystyle \lim_{ten→1}(2x+1)=3\).

Afterwards removing all the remarks, hither is a last version of the proof:

Let \(ε>0\).

Choose \(δ=ε/2\).

Assume \(0<|x−ane|<δ\).

In other words:

\(0<|x−i|<\frac{ε}{2}\),

so \(-\frac{ε}{2}<x−1<\frac{ε}{ii}\),

then \(-ε<2x−two<ε\)

so |\(2x−2|<ε\),

and then |(\(2x+ane)−iii\)|<ε

Thus, if \(0<|x−one|<δ\), then |(\(2x+one)−3\)|<ε.

Therefore, by the definition of limit, \(\displaystyle \lim_{ten→1}(2x+one)=3\).

The following Problem-Solving Strategy summarizes the type of proof we worked out in Case \(\PageIndex{1}\).

Problem-Solving Strategy: Proving That \(\displaystyle \lim_{x→a}f(x)=Fifty\) for a Specific Function \(f(x)\)

1. Let'due south begin the proof with the following statement: Let \(ε>0\).
2. Side by side, nosotros need to obtain our option for \(δ\) (utilise the Analysis Doodle). The Analysis Doodle is scratch piece of work done to detect our pick for \(δ\). Always put it on a separate page, or in a box marked "Scratch Work". Brand the post-obit argument, filling in the blank with our discovered pick of δ: Choose \(δ=\)_______.
3. The next statement in the proof should be (at this point, nosotros make full in our given value for a): Assume \(0<|ten−a|<δ\).
4. Starting with \(0<|ten−a|<δ\), apply our choice of \(δ\) and algebra to lead to \(|f(10)−L|<ε\), where \(f(10)\) and Fifty are our function \(f(x)\) and our limit L.
5. This shows (and y'all should state) if \(0<|ten−a|<δ\), then \(|f(x)−L|<ε\).
6. We conclude our proof with the argument: Therefore, by the definition of limit, \(\displaystyle \lim_{x→a}f(10)=L\).

Example \(\PageIndex{2}\): Proving a Argument about a Limit

Complete the proof that \(\displaystyle \lim_{x→−1}(4x+1)=−3\) by filling in the blanks.

Let _____.

Choose \(δ=\)_______.

Assume \(0<\)|\(10\)−_______|\(<δ\).

In other words, |\(x\)−_______|\(<\) _______, then _______________ then ________________ then _______________ ... then __________\(<ε\).

Thus, if ____________________________, then ________________.

Therefore, by _______________________________ _____________________________.

Solution

We begin by filling in the blanks where the choices are specified by the definition. Thus, nosotros accept

Let ε\(>0\).

---

SCRATCH WORK:

Cull \(δ\)= ??.

Here is our Analysis Doodle:

Nosotros desire \(|4x+1 -(-3)|\) to be less than \(ε\), if \(0<\)|\(x−(−ane)\)|\(<δ\).

So, we set up \(|4x+1 -(-3)|<ε \) and fiddle around to get \(10−(−1)\) within the absolute value.

\(|4x+i -(-3)|<ε \) implies \(-ε<4x+iv<ε \) implies \(-\frac{ε}{4}<x+1<\frac{ε}{iv} \) implies \(|ten+1|<\frac{ε}{4} \)

Thus we see that we should choose \(δ=\frac{ε}{four}\).

Nosotros now consummate the final write-up of the proof:

---

Let ε\(>0\).

Choose \(δ=\frac{ε}{4}\).

Assume \(0<\)|\(ten−(−ane)\)|\(<δ\) (or equivalently, \(0<\)|\(x+1\)|\(<δ\).)

In other words:

\(0<|x+1|<\frac{ε}{iv}\),

so \(-\frac{ε}{4}<x+1<\frac{ε}{four}\),

then \(-ε<4x+four<ε\)

and then |\(4x+4|<ε\),

and then |(\(4x+ane)−(-3)\)|<ε

Thus, if \(0<|x−(-ane)|<δ\), then |(\(4x+1)−(-iii)\)|<ε.

Therefore, by the definition of limit, \(\displaystyle \lim_{x→-1}(4x+1)=-3\).

\(\PageIndex{1}\)

Complete the proof that \(\displaystyle \lim_{x→2}(3x−2)=4\) by filling in the blanks. (Your Analysis Doodle is Non written in the actual proof.)

Allow _______.

Choose \(δ\) =_______.

Presume \(0<\)|\(x−\)____|\(<\)____.

In other words, |\(10\)−_______|\(<\) _______, then _______________ then ________________ then _______________ ... and so __________\(<ε\).

Thus, if ____________________________, then ________________.

Therefore, by _______________________________ _____________________________.

Hint

Follow the outline in the Problem-Solving Strategy that nosotros worked out in total in Example \(\PageIndex{ii}\).

Answer

Allow ε\(>0\); choose \(δ=\frac{ε}{3}\); presume \(0<|10−two|<δ\).

In other words:

\(0<|x - 2|<\frac{ε}{3}\),

so \(-\frac{ε}{3}<10 - two<\frac{ε}{three}\),

then \(-ε<3x - 6<ε\)

and so |\(3x - 6|<ε\),

then |(\(3x - 2)−4\)|<ε

Thus, if \(0<|ten−two|<δ\), then |(\(3x - 2)−4\)|<ε.

Therefore, by the definition of limit, \(\displaystyle \lim_{ten→ii}3x−2=iv\).

---

Precise Definitions for Limits at Infinity

Earlier, nosotros used the terms arbitrarily close, arbitrarily large, and sufficiently large to define limits at infinity informally. Although these terms provide accurate descriptions of limits at infinity, they are not precise mathematically. Here are more formal definitions of limits at infinity. We and then look at how to use these definitions to evidence results involving limits at infinity.

Definition: Limit at Infinity (Formal)

Nosotros say a function \(f\) has a limit at infinity, if in that location exists a real number \(L\) such that for all \(ε>0\), in that location exists \(Northward>0\) such that

\[|f(x)−L|<ε\]

for all \(ten>N.\) in that case, nosotros write

\[\lim_{x→∞}f(ten)=L\]

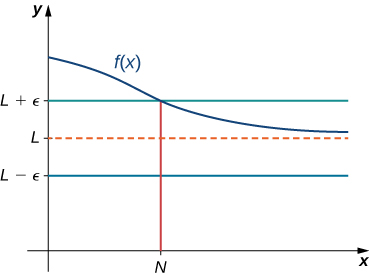
Figure \(\PageIndex{iii}\): For a role with a limit at infinity, for all \(x>Northward, |f(ten)−L|<ε.\)

Earlier in this section, we used graphical evidence in Figure and numerical evidence in Tabular array to conclude that \(\lim_{x→∞}(\frac{2+1}{x})=2\). Hither nosotros utilise the formal definition of limit at infinity to evidence this result rigorously.

Example \(\PageIndex{3}\):

Utilise the formal definition of limit at infinity to prove that \(\displaystyle \lim_{10→∞}two+\frac{i}{x}=2\).

Solution

Permit \(ε>0.\) Let \(N=\frac{ane}{ε}\). Therefore, for all \(x>N\), we take

\[|ii+\frac{1}{x}−2|=|\frac{1}{x}|=\frac{1}{ten}<\frac{ane}{N}=ε\]

Therefore, \(\displaystyle \lim_{x→∞}ii+\frac{1}{x}=2\).

\(\PageIndex{2}\)

Utilise the formal definition of limit at infinity to prove that \(\displaystyle \lim_{x→∞}3−\frac{ane}{x^2}=3\).

Hint

Let \(N=\frac{1}{\sqrt{ε}}\).

Respond

Let \(ε>0.\) Let \(N=\frac{1}{\sqrt{ε}}\). Therefore, for all \(x>N,\) nosotros have

\(∣3−\frac{1}{x^2}−3∣=\frac{1}{x^two}<\frac{1}{N^two}=ε\)

Therefore, \(\displaystyle \lim_{x→∞}(3−\frac{1}{ten^ii})=3.\)

We at present turn our attention to a more precise definition for an infinite limit at infinity.

Definition: Infinite Limit at Infinity (Formal)

We say a role \(f\) has an space limit at infinity and write

\(\displaystyle \lim_{x→∞}f(x)=∞\)

if for all \(M>0,\) at that place exists an \(N>0\) such that

\(f(x)>Thousand\)

for all \(10>N\) (run across Effigy).

We say a function has a negative space limit at infinity and write

\(\displaystyle \lim_{x→∞}f(x)=−∞\)

if for all \(1000<0\), in that location exists an \(N>0\) such that

\(f(ten)<Grand\)

for all \(ten>North\).

Similarly we tin can define limits as \(ten→−∞.\)

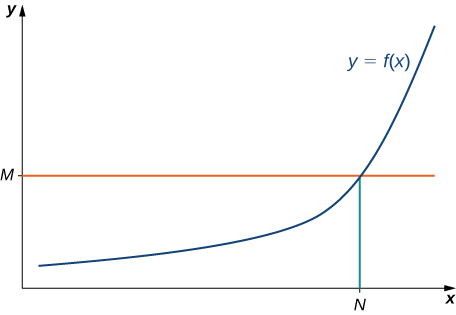
Figure \(\PageIndex{4}\): For a role with an infinite limit at infinity, for all \(x>North, f(x)>M.\)

Hither we use the formal definition of space limit at infinity to prove \(\displaystyle \lim_{x→∞}x^3=∞\).

Instance \(\PageIndex{4}\):

Use the formal definition of space limit at infinity to prove that \(\displaystyle \lim_{ten→∞}x^3=∞.\)

Doodle Analysis: For some \(M>0\), we need an \(N\) and then that if \(x>N\), we get \(ten^3>G\).

Offset with \(x^three>1000\), and solve for \(ten\). \(10>\sqrt[3]{G}\). And then, as long every bit \(x>\sqrt[3]{M}\), then \(x^iii>Thousand\). So, choose \(N=\sqrt[3]{M}\).

Proof:

Permit \(Grand>0.\) Choose \(N=\sqrt[3]{Thou}\). Then, for all \(x>North\), nosotros have

\(x^3>N^3=(\sqrt[three]{M})^three=Yard.\)

Therefore, by the definition of limit, \(\displaystyle \lim_{x→∞}ten^three=∞\).

\(\PageIndex{3}\)

Use the formal definition of infinite limit at infinity to show that \(\displaystyle \lim_{x→∞}3x^2=∞.\)

Hint

Let \(Northward=\sqrt{\frac{Grand}{three}}\).

Reply

Let \(M>0.\) Permit \(North=\sqrt{\frac{M}{3}})\). Then, for all \(x>N,\) we have

\(3x^two>3N^two=3(\sqrt{\frac{M}{3}})^22=\frac{3M}{3}=M\)

---

I-Sided Limits

Just as we outset gained an intuitive agreement of limits and then moved on to a more than rigorous definition of a limit, we now revisit i-sided limits. To do this, nosotros modify the epsilon-delta definition of a limit to give formal epsilon-delta definitions for limits from the right and left at a bespeak. These definitions only crave slight modifications from the definition of the limit. In the definition of the limit from the right, the inequality \(0<ten−a<δ\) replaces \(0<|x−a|<δ\), which ensures that we only consider values of x that are greater than (to the right of) a. Similarly, in the definition of the limit from the left, the inequality \(−δ<10−a<0\) replaces \(0<|x−a|<δ\), which ensures that we just consider values of x that are less than (to the left of) a.

Definition

Limit from the Correct: Allow \(f(10)\) be divers over an open interval of the form \((a,b)\) where \(a<b\). Then

\[\lim_{x→a^+}f(ten)=Fifty\]

if for every \(ε>0\), there exists a \(δ>0\), such that if \(0<x−a<δ\), then \(|f(x)−L|<ε\).

Limit from the Left: Allow \(f(ten)\) be divers over an open up interval of the form \((b,c)\) where \(b<c\). Then,

\[\lim_{ten→c^−}f(x)=L\]

if for every \(ε>0\), there exists a \(δ>0\) such that if \( −δ<x−c<0\), so \(|f(ten)−L|<ε\).

Instance \(\PageIndex{5}\): Proving a Statement nigh a Limit From the Right

Bear witness that

\[lim_{x→iv^+}\sqrt{x−four}=0.\]

Solution

Let ε>0.

Cull \(δ=ε^2\). Since we ultimately want \(∣\sqrt{10−4}−0∣<ε\), we manipulate this inequality to go \(\sqrt{ten−4}<ε\) or, equivalently, \(0<x−4<ε^ii\), making \(δ=ε^two\) a clear selection.

Assume \(0<x−4<δ\). Thus, \(0<ten−4<ε^two\). Hence, \(0<\sqrt{10−4}<ε\). Finally, \(∣\sqrt{x−4}−0∣<ε\). Therefore, \(\displaystyle \lim_{10→iv^+}\sqrt{ten−4}=0\).

\(\PageIndex{iv}\)

Find \(δ\) respective to \(ε\) for a proof that \(\displaystyle \lim_{ten→1^−}\sqrt{1−x}=0\).

Hint

Sketch the graph and employ Example as a solving guide.

Answer

\(δ=ε^2\)

Infinite Limits

Nosotros conclude the procedure of converting our intuitive ideas of various types of limits to rigorous formal definitions by pursuing a formal definition of space limits. To have \(\displaystyle \lim_{10→a}f(x)=+∞\), nosotros want the values of the part \(f(10)\) to go larger and larger as x approaches a. Instead of the requirement that \(|f(x)−L|<ε\) for arbitrarily minor \(ε\) when \(0<|x−a|<δ\) for small enough \(δ\), we want \(f(ten)>M\) for arbitrarily large positive M when \(0<|ten−a|<δ\) for pocket-sized enough \(δ\). Figure illustrates this idea by showing the value of \(δ\) for successively larger values of G.

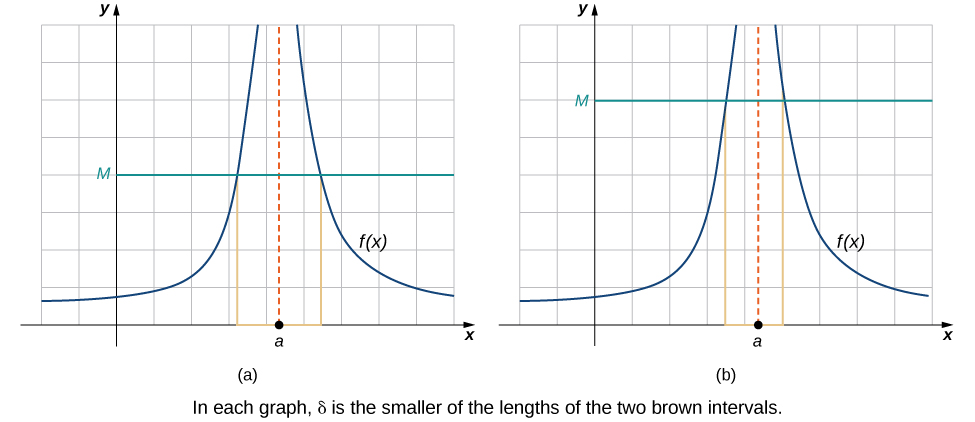
Figure \(\PageIndex{v}\): These graphs plot values of \(δ\) for M to prove that \(\displaystyle \lim_{x→a}f(10)=+∞\).

Definition

Let \(f(x)\) be defined for all \(x≠a\) in an open interval containing a. And then, we have an infinite limit

\[\lim_{x→a}f(10)=+∞\]

if for every \(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), and so \(f(x)>M\).

Let \(f(ten)\) be divers for all \(x≠a\) in an open interval containing a. Then, nosotros have a negative infinite limit

\[\lim_{10→a}f(x)=−∞\]

if for every \(G>0\), there exists \(δ>0\) such that if \(0<|ten−a|<δ\), then \(f(x)<−M\).

Advanced Topics

Here are some more complex problems using the precise definition of limit. Feel free to expect these over; however, y'all are not required to know the remaining topics in this department.

---

In Examples \(\PageIndex{1}\) and \(\PageIndex{2}\), the proofs were fairly straightforward, since the functions with which we were working were linear. In Example, nosotros see how to modify the proof to accommodate a nonlinear role.

Case \(\PageIndex{6}\):Proving a Argument about the Limit of a Quadratic Function

Bear witness that \(\displaystyle \lim_{x→−i}(x^two−2x+3)=6.\)

Solution

Let'southward use our outline from the Trouble-Solving Strategy:

1. Let \(ε>0\).

ii. Choose \(δ=min\){\(i,ε/5\)}. This choice of \(δ\) may appear odd at first glance, but it was obtained by taking a look at our ultimate desired inequality: ∣\((10^2−2x+iii)−6\)∣\(<ε\). This inequality is equivalent to \(|x+1|⋅|x−3|<ε\). At this point, the temptation simply to choose \(δ=\frac{ε}{x−3}\) is very stiff. Unfortunately, our choice of \(δ\) must depend on ε merely and no other variable. If nosotros can supersede \(|x−3|\) by a numerical value, our problem can be resolved. This is the identify where assuming \(δ≤1\) comes into play. The option of \(δ≤one\) here is capricious. We could have but as hands used whatever other positive number. In some proofs, greater care in this choice may be necessary. Now, since \(δ≤1\) and \(|x+one|<δ≤one\), we are able to show that \(|ten−three|<5\). Consequently, \(|ten+i|⋅|x−3|<|x+one|⋅5\). At this bespeak we realize that we too need \(δ≤ε/5\). Thus, nosotros cull \(δ=min\){\(1,ε/5\)}.

3. Presume \(0<|x+ane|<δ\). Thus,

\[|x+i|<ane\] and \[|ten+1|<\frac{ε}{5}.\]

Since \(|x+1|<one\), nosotros may conclude that \(−i<ten+1<1\). Thus, by subtracting 4 from all parts of the inequality, we obtain \(−5<10−iii<−one\). Consequently, \(|10−three|<5\). This gives us

\[∣(x^ii−2x+3)−vi∣=|10+1|⋅|x−three|<\frac{ε}{5}⋅5=ε.\]

Therefore,

\[\displaystyle \lim_{x→−1}(x^ii−2x+iii)=vi.\]

\(\PageIndex{five}\)

Consummate the proof that \(\displaystyle \lim_{x→1}x^ii=1\).

Let \(ε>0\); choose \(δ=min\){\(1,ε/3\)}; presume \(0<|x−1|<δ\).

Since \(|ten−1|<1\), nosotros may conclude that \(−1<x−1<1\). Thus, \(1<x+one<3\). Hence, \(|x+1|<3\).

Hint

Apply Example as a guide.

Reply

\(∣x^ii−one∣=|x−1|⋅|x+1|<ε/3⋅3=ε\)

Proving Limit Laws

Nosotros now demonstrate how to use the epsilon-delta definition of a limit to construct a rigorous proof of one of the limit laws. The triangle inequality is used at a key betoken of the proof, so nosotros first review this central holding of absolute value.

Definition

The triangle inequality states that if a and b are whatsoever real numbers, and so \(|a+b|≤|a|+|b|\).

proof

We prove the following limit law: If \(\displaystyle \lim_{x→a}f(ten)=L\) and \(\displaystyle \lim_{x→a}yard(ten)=K\), and so \(\displaystyle \lim_{x→a}(f(10)+thou(x))=L+M\).

Let \(ε>0\).

Choose \(δ_1>0\) so that if \(0<|ten−a|<δ_1\), and then \(|f(x)−L|<ε/2\).

Choose \(δ_2>0\) so that if \(0<|x−a|<δ_2\), so \(|thou(x)−M|<ε/2\).

Choose \(δ=min\){\(δ_1,δ_2\)}.

Assume \(0<|x−a|<δ\).

Thus,

\(0<|x−a|<δ_1\) and \(0<|10−a|<δ_2\).

Hence,

\(|(f(10)+g(ten))−(L+G)|=|(f(10)−L)+(k(10)−M)|\)

\(≤|f(x)−L|+|one thousand(x)−M|\)

\(<\frac{ε}{2}+\frac{ε}{two}=ε\).

□

Nosotros now explore what it means for a limit non to be. The limit \(\displaystyle \lim_{x→a}f(x)\) does non be if in that location is no real number 50 for which \(\displaystyle \lim_{x→a}f(x)=L\). Thus, for all existent numbers L, \(\displaystyle \lim_{10→a}f(x)≠L\). To sympathize what this ways, we expect at each office of the definition of \(\displaystyle \lim_{x→a}f(x)=L\) together with its contrary. A translation of the definition is given in Table.

Definition	Reverse
1. For every \(ε>0\),	1. There exists \(ε>0\) so that
two. there exists a \(δ>0\), so that	2. for every \(δ>0\),
3. if \(0<|x−a|<δ\), then \(|f(10)−L|<ε\).	3. In that location is an x satisfying \(0<|x−a|<δ\) and then that \(|f(x)−L|≥ε\).

Finally, nosotros may country what it ways for a limit not to exist. The limit \(\displaystyle \lim_{ten→a}f(x)\) does not exist if for every real number Fifty, in that location exists a real number \(ε>0\) then that for all \(δ>0\), there is an 10 satisfying \(0<|ten−a|<δ\), so that \(|f(x)−L|≥ε\). Let's apply this in Example to evidence that a limit does non exist.

Example \(\PageIndex{7}\): Showing That a Limit Does Non Exist

Bear witness that \(\displaystyle \lim_{x→0}\frac{|x|}{x}\) does non exist. The graph of \(f(x)=|10|/x\) is shown hither:

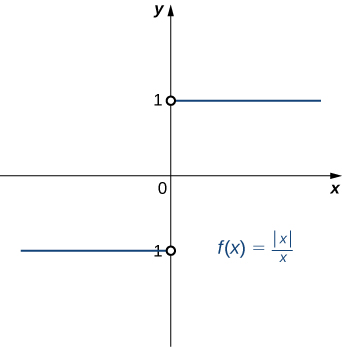
Solution

Suppose that 50 is a candidate for a limit. Cull \(ε=i/2\).

Let \(δ>0\). Either \(L≥0\) or \(Fifty<0\). If \(L≥0\), then let \(ten=−δ/2\).

Thus,

\(|x−0|=∣−\frac{δ}{ii}−0∣=\frac{δ}{two}<δ\)

and

\(∣\frac{∣−\frac{δ}{2}∣}{−\frac{δ}{2}}−Fifty∣=|−ane−L|=L+1≥1>\frac{1}{2}=ε\).

On the other manus, if \(L<0\), then permit \(x=δ/ii\). Thus,

\(|10−0|=∣\frac{δ}{2}−0∣=\frac{δ}{ii}<δ\)

and

\(∣\frac{∣\frac{δ}{ii}∣}{\frac{δ}{two}}−L∣=|one−Fifty|=|L|+1≥1>\frac{i}{ii}=ε\).

Thus, for any value of L, \(\displaystyle \lim_{x→0}\frac{|10|}{x}≠L.\)

Key Concepts

• The intuitive notion of a limit may exist converted into a rigorous mathematical definition known equally the epsilon-delta definition of the limit.
• The epsilon-delta definition may be used to evidence statements about limits.
• The epsilon-delta definition of a limit may exist modified to define one-sided limits.

Glossary

epsilon-delta definition of the limit

\(\displaystyle \lim_{x→a}f(x)=L\) if for every \(ε>0\), there exists a \(δ>0\) such that if \(0<|10−a|<δ\), then \(|f(x)−L|<ε\)

triangle inequality

If a and b are any existent numbers, so \(|a+b|≤|a|+|b|\)

Contributors

• Gilbert Strang (MIT) and Edwin "Jed" Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-By-SA-NC four.0 license. Download for free at http://cnx.org.

jimenezforld1988.blogspot.com

Source: https://math.libretexts.org/Courses/Monroe_Community_College/MTH_210_Calculus_I_(Professor_Dean)/Chapter_2_Limits/2.7%3A_The_Precise_Definition_of_a_Limit

Share this post